习题选讲
验证 u(x,t) = F(x + at) + G(x - at) 是振动方程 u_{tt} - a^2 u_{xx} = 0 的通解,其中 F,G 是任意的二阶可微函数。
解:由链式法则
容易得到 u_{tt} - a^2 u_{xx} = 0,表明 u(x,t) = F(x + at) + G(x - at) 是振动方程的解。
下面证明是通解:
令 (x,t) \to (\xi, \eta) 满足 \xi = x + at, \eta = x - at,由链式法则:
代入方程 u_{tt} - a^2 u_{xx} = 0,得到 -4a^2 u_{\xi\eta} = 0 或 u_{\xi\eta} = 0。
上述推导表明,u_{tt} - a^2 u_{xx} = 0 \Leftrightarrow u_{\xi\eta} = 0,于是开始积分:
改写原方程为 u(\xi, \eta) = F(\xi) + G(\eta),是 u_{\xi\eta} = 0 的通解。
那么 u(x,t) = F(x + at) + G(x - at) 也是振动方程 u_{tt} - a^2 u_{xx} = 0 的通解,其中 F(x + at), G(x - at) 分别是左行波和右行波,a 是行波速度。
二阶线性偏微分方程的化简与分类
一般形式
A u_{xx} + 2B u_{xy} + C u_{yy} + D u_x + E u_y + F u = 0 或 f
其中 A,B,C,\ldots 是 (x,y) 的已知函数或者常数,且 A,B,C 不全为 0,u = u(x,y) 是未知函数。
通常情况下,称二阶导数部分为"主要部分",其余部分简记为 H。于是方程改写为 A u_{xx} + 2B u_{xy} + C u_{yy} = H。
判别式 \Delta
定义 \Delta = (2B)^2 - 4AC = 4(B^2 - AC),可用"特征线方法"简化方程。
利用理论,方程具有以下形式的特征方程:A (dy)^2 - 2B dx dy + C (dx)^2 = 0。
方程的解(曲线)称为特征线。利用"特征线"可以适当对方程进行简化,并进行分类:
- \Delta > 0,双曲型
- \Delta < 0,椭圆型
- \Delta = 0,抛物型
分类与化简
常系数情形
a_{11} u_{xx} + 2a_{12} u_{xy} + a_{22} u_{yy} = H,其中 a_{11}, a_{12}, a_{22} \in \mathbb{R},H 是低阶项部分。
令 A = \begin{pmatrix} a_{11} & a_{12} \\ a_{12} & a_{22} \end{pmatrix},是一个对称矩阵,对应一个二次型 \left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y} \right) A \begin{pmatrix} \frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} \end{pmatrix} u = H,存在正交变换 (x,y) \to (\xi,\eta),满足
于是在这个变换下,u(\xi,\eta) 满足方程 \lambda_1 u_{\xi\xi} + \lambda_2 u_{\eta\eta} = \tilde{H},其中 \lambda_1, \lambda_2 是矩阵 A 的特征值。有以下三种情况:
- \lambda_1 \lambda_2 > 0,这时 \Delta < 0,令 \alpha = \frac{1}{\sqrt{\lambda_1}} \xi, \beta = \frac{1}{\sqrt{\lambda_2}} \eta,则方程可以简化为 u_{\alpha\alpha} + u_{\beta\beta} = \tilde{\tilde{H}},其主部是拉普拉斯方程,对应椭圆型。
- \lambda_1 \lambda_2 = 0,这时 \Delta = 0,令 \alpha = \frac{1}{\sqrt{\lambda_1}} \xi, \beta = \eta,则方程可以简化为 u_{\alpha\alpha} = \tilde{\tilde{H}} \triangleq b_1 u_\alpha + b_2 u_\beta + c u,其主部是热传导方程。进一步可以简化为 u_\beta - a^2 u_{\alpha\alpha} = 0 或 f,左边称为导热算子,或热传导的标准型。
- \lambda_1 \lambda_2 < 0,这时 \Delta > 0,不妨设 \alpha = \frac{1}{\sqrt{\lambda_1}} \xi, \beta = \frac{1}{\sqrt{-\lambda_2}} \eta,则方程简化为 u_{\alpha\alpha} - u_{\beta\beta} = \tilde{\tilde{H}},其主部是波动方程。
变系数情形
a_{11} u_{xx} + 2a_{12} u_{xy} + a_{22} u_{yy} = H,其中 a_{11}, a_{12}, a_{22} 是关于 x,y 的函数。
这时,矩阵 A 是函数矩阵,不再适用"二次型正交变换",因为经过链式法则,得到的是同样复杂、形式相近的式子。比如令 \xi = \xi(x,y), \eta = \eta(x,y),方程可化为 \bar{a}_{11} u_{\xi\xi} + 2\bar{a}_{12} u_{\xi\eta} + \bar{a}_{22} u_{\eta\eta} = \bar{H},其中
如果取一阶偏微分方程 a_{11} \varphi_x^2 + 2a_{12} \varphi_x \varphi_y + a_{22} \varphi_y^2 = 0 的一个特解作为新自变量 \xi = \xi(x,y),则 \bar{a}_{11} = 0,类似的,如果取另一个特解作为自变量 \eta,则 \bar{a}_{22} = 0,从而方程得以化简。
注意到 a_{11} \varphi_x^2 + 2a_{12} \varphi_x \varphi_y + a_{22} \varphi_y^2 = 0 的求解可以化为常微分方程求解:将方程变形为 a_{11} \left( -\frac{\varphi_x}{\varphi_y} \right)^2 - 2a_{12} \left( -\frac{\varphi_x}{\varphi_y} \right) + a_{22} = 0,由隐函数导数理论,可以得到 a_{11} \left( \frac{dy}{dx} \right)^2 - 2a_{12} \left( \frac{dy}{dx} \right) + a_{22} = 0,或写为 a_{11} dy^2 - 2a_{12} dx dy + a_{22} dx^2 = 0,称为二阶线性偏微分方程的特征方程,特征方程的解称为特征线。
解方程
理论
分三种情况来处理:双曲、椭圆、抛物。解方程没有理论部分难。
(i) 双曲型.
在点 (x_0, y_0) 的领域内,判别式
此时方程(4.17)有两族积分曲线,分别由下述两个方程
确定。假设它们的解分别是 \{\varphi_1(x,y) = c\} 及 \{\varphi_2(x,y) = c\},从而有:
由 \Delta = a_{12}^2 - a_{11}a_{22} > 0,得到 \frac{\varphi_{1x}}{\varphi_{1y}} \neq \frac{\varphi_{2x}}{\varphi_{2y}},即变换的 Jacobi 行列式
故变换(4.16)是可逆的,且在此变换下,方程(4.1.2)可化为
其中方程的系数均为 \xi, \eta 的函数。如果再作自变量的变换
则方程进一步化为
的形式。
(ii) 抛物型。
在点 (x_0, y_0) 的一邻域中 \Delta = a_{12}^2 - a_{11}a_{22} \equiv 0,并且 a_{11}, a_{12}, a_{22} 不全为零,此时可不妨设 a_{11} 与 a_{22} 同号,方程可表示为完全平方形式:
故特征曲线只有一族,记为 \varphi_1(x, y) = c。选取 \xi = \varphi_1(x, y)。由于 \Delta \equiv 0,因此
因此,无论函数 \eta = \varphi_2(x, y) 如何选取,经变换后方程中 \bar{a}_{11} 及 \bar{a}_{12} 同时为零,从而我们可任选一个与 \varphi_1(x, y) 函数无关的函数 \eta = \varphi_2(x, y),即在 (x_0, y_0) 附近满足 \left| \frac{\partial (\varphi_1,\varphi_2)}{\partial (x,y)} \right| \neq 0,通过变换,方程就化为
的形式。如果在方程(4.22)中再作未知函数的线性变换
就得到关于 v 的方程
其中不再出现关于 \eta 的一阶偏导数项。
(iii) 椭圆型。
在点 (x_0, y_0) 的附近 \Delta = a_{12}^2 - a_{11}a_{22} < 0。此时不存在实的特征线,方程(4.17)的通积分只能是复函数。因而二次方程无实值解,但有两个复共轭解,它们是实变量 x 和 y 的复值函数。
假设
是 (4.18) 式的一个通积分,即满足 a_{11}\varphi_x = -\left(a_{12} + \sqrt{a_{12}^2 - a_{11}a_{22}}\right)\varphi_y,并且 \varphi_x, \varphi_y 不同时为零,这里 \varphi_1, \varphi_2 是实的函数。为了避免引入复函数,我们作变换
可以证明,\varphi_1(x,y) 和 \varphi_2(x,y) 是函数无关的。事实上,因为 \varphi(x,y) = c ,故
把实部及虚部分开,得到
由于 a_{11} \neq 0 (否则 \Delta 不会小于零),成立
这个行列式的值不等于零,否则就会推出 \xi_y = \eta_y = 0,再由前式就得出 \xi_x = \eta_x = 0,从而 \varphi_x = \varphi_y = 0,但这与关于函数 \varphi 的假定不符。因此变换中的 \varphi_1, \varphi_2 是函数无关的。
由于 \xi + i\eta 满足方程 (4.15),代入后将实部及虚部分开,得到
因此,由知:方程化为
的形式。
例题





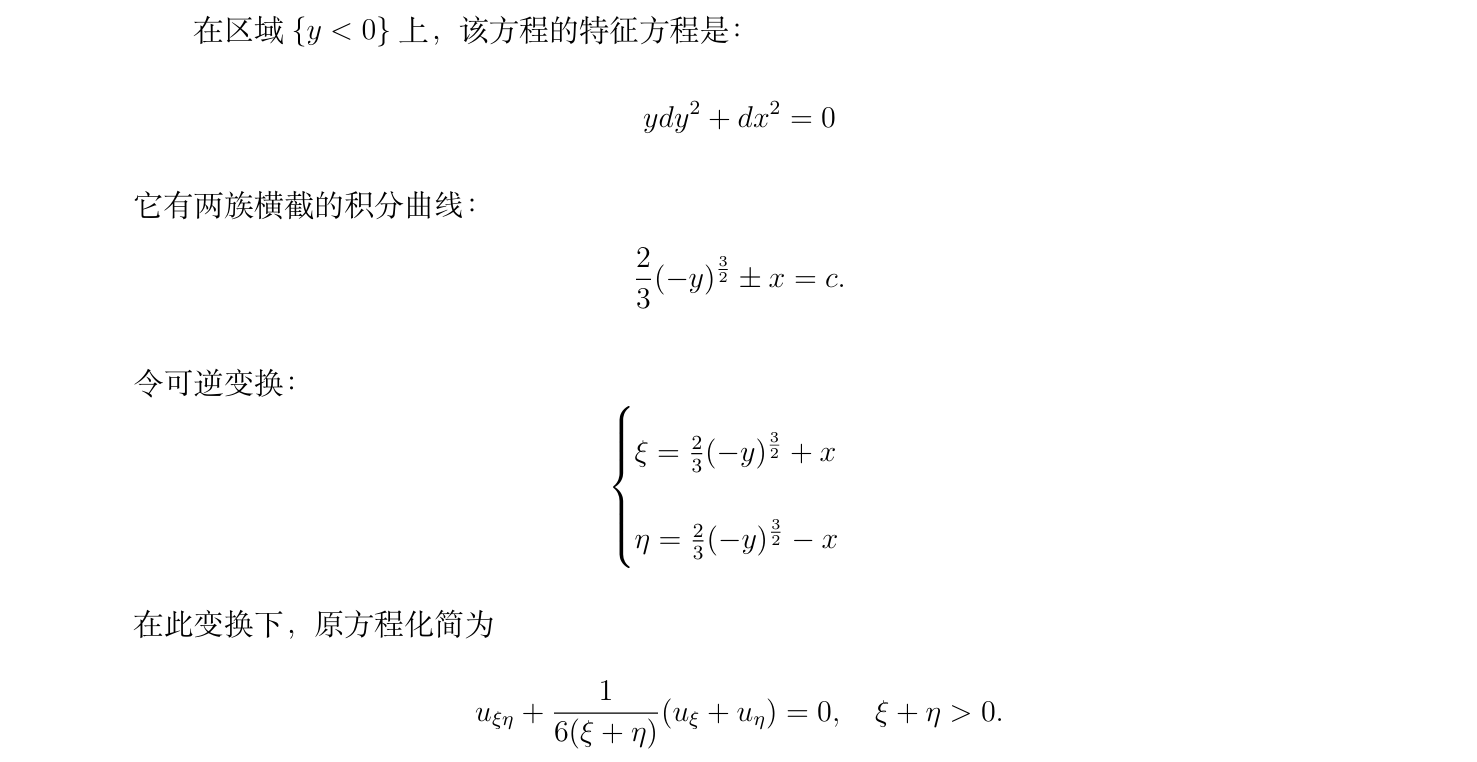

达朗贝尔解双曲型


分离变量法






默认评论
Halo系统提供的评论