简介

逻辑回归，又称logistic回归，常用于解决二分类或者多分类的问题。想象一下线性回归：y = wx + b。它输出一个连续的、可以是任意大小的数值。如果我们想用它来预测一个类别（例如：0或1，是或否），直接使用它的输出是不合适的。

因此，我们要想办法找一个函数，将线性回归的结果映射到一个介于0和1之间的值，这里记作p。当p>0.5时判定为1，反之判定为0。如此一来，就可以实现训练模型-输入数据-获得分类结果。

通常情况下，逻辑回归是一个线性模型，当然，也可以调整成非线性的，本文只讨论线性模型的情况，且直接讨论通用形式，不对二维情形做单独的讨论。

理论部分：数学推导与模型介绍

Sigmoid函数

sigmoid函数的公式如下：

它的图像是一个优美的“S”型曲线：

• 当z \to + \infty 时，输出\sigma (z) 无限接近 1。
• 当z \to - \infty 时，输出\sigma (z) 无限接近 0。
• 当 z=0 时，\sigma (z) = 0.5

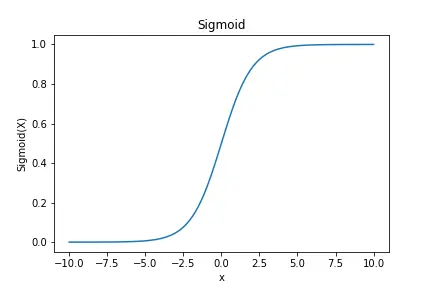
这个特性完美地将任何实数转换成了(0,1)区间的值，我们可以将其解释为概率。

逻辑回归模型

在逻辑回归中，我们将线性回归的输出 z = {\omega _0} + {\omega _1}{x_1} + {\omega _2}{x_2} + \cdots + {\omega _n}{x_n}作为Sigmoid函数的输入。

令{\underline \omega ^T} = \left[ {{\omega _0},{\omega _1},{\omega _2}, \cdots ,{\omega _n}} \right]，\underline x = \left[ {1,{x_0},{x_1}, \cdots ,{x_n}} \right]，则z = {\underline \omega ^T}\underline x

之后，将z代入Sigmoid函数，得到预测概率

决策边界

我们得到了一个概率，如何最终做出分类决策呢？我们需要设定一个阈值，通常默认为0.5：

• \hat y \ge 0.5，预测为1
• \hat y < 0.5，预测为0

由于Sigmoid函数在 z=0 时输出0.5，所以这个决策规则等价于：

• {\underline \omega ^T}\underline x \ge 0，预测为1
• {\underline \omega ^T}\underline x < 0，预测为0

这个{\underline \omega ^T}\underline x 就是一个决策边界，在二维空间中是一条直线，在三维空间中是一个平面，在高维空间中是一个超平面。逻辑回归的本质就是通过学习参数\underline \omega 来找到这个最佳决策边界。

损失函数

模型需要学习，就必须有一个衡量预测好坏的指标，这就是损失函数。线性回归用的是均方误差，但它在逻辑回归中不是一个好的选择（会导致非凸优化问题，容易陷入局部最优）。

逻辑回归使用 交叉熵损失函数。

对于单个样本，其损失函数定义为：

• 当真实标y=1 时，损失函数变为- {\log \left( {\hat y} \right)}。如果预测概率{\hat y}越接近1，损失 越- {\log \left( {\hat y} \right)}接近0（预测正确）；如果 {\hat y} 越接近0，损失 - {\log \left( {\hat y} \right)}会变得非常大（惩罚预测错误）。
• 当真实标签 y=0 时，损失函数变为 {-\log \left( {1 - \hat y} \right)}。如果预测概率 \hat y 越接近0，损失越接近0；如果 \hat y 越接近1，损失会变得非常大。

代价函数

定义平均交叉熵损失（代价函数）：

其中L(\hat{y}^{(i)},y^{(i)})=-[y^{(i)}\log(\hat{y}^{(i)})+(1-y^{(i)})\log(1-\hat{y}^{(i)})]是单个样本的损失，\hat{y}^{(i)}=\sigma(z^{(i)})=\frac{1}{1+e^{-z^{(i)}}}是模型的预测输出。

参数学习：梯度下降法

我们的目标是找到\underline \omega ^T，使得总的代价函数（平均交叉熵损失）最小化。

这个过程通常通过梯度下降算法来实现。其核心思想是：

1. 初始化参数 \underline \omega ^T
2. 计算代价函数对每个参数的梯度（偏导数）。
3. 沿着梯度的反方向（即下降最快的方向）更新参数。
4. 重复步骤2和3，直到代价函数收敛或达到预设的迭代次数。

参数更新公式如下：

其中 \alpha是学习率，控制每次更新的步长。

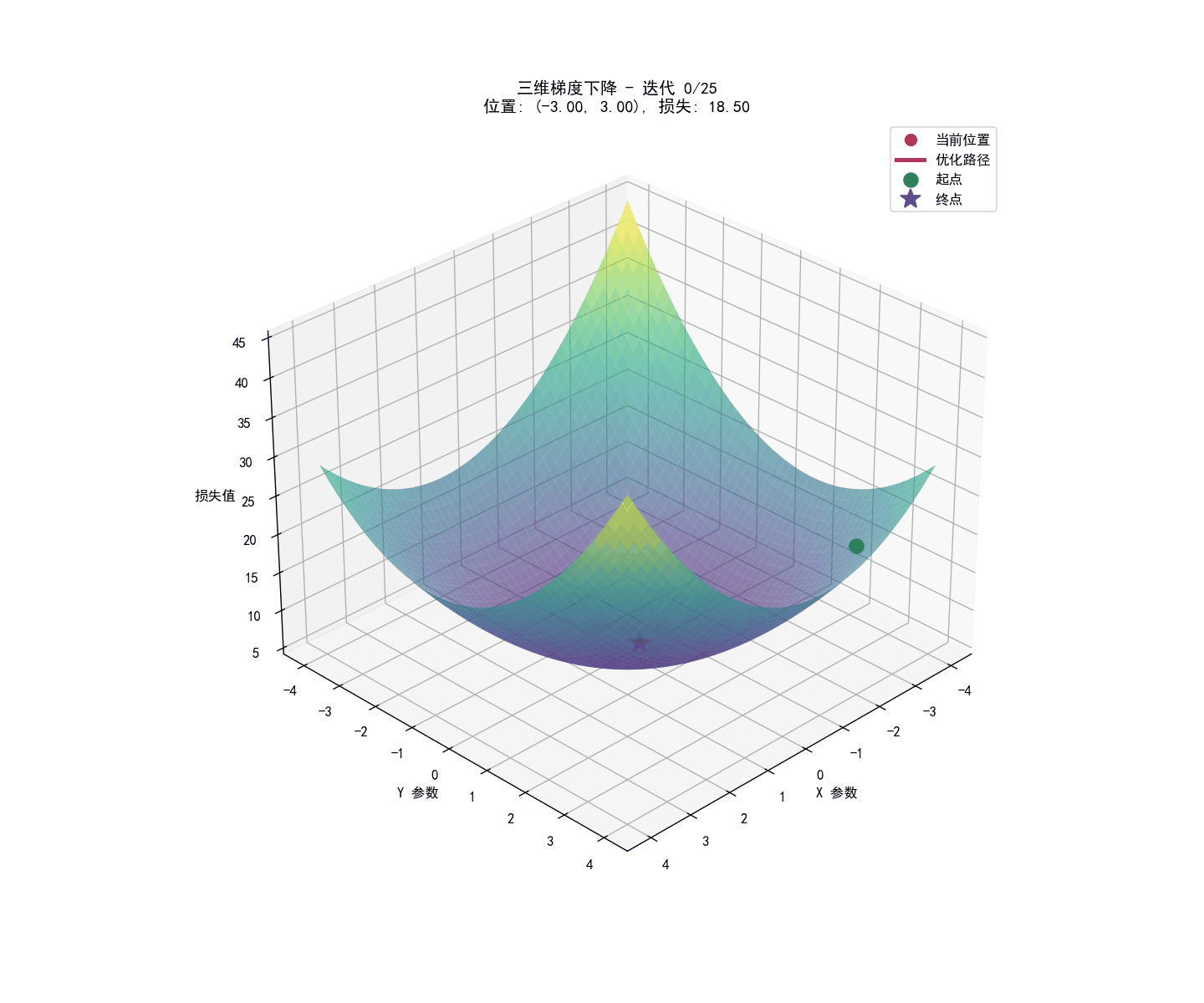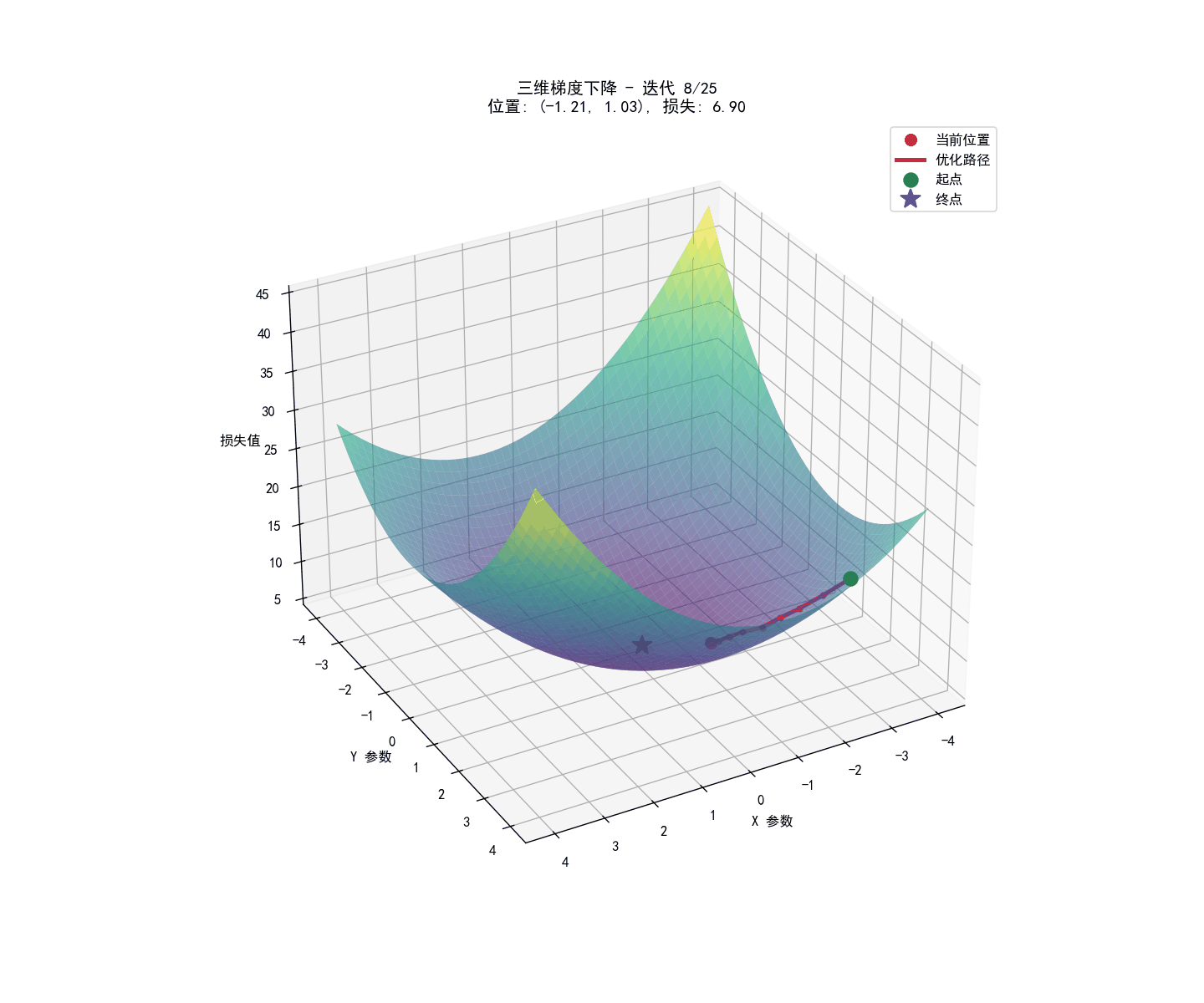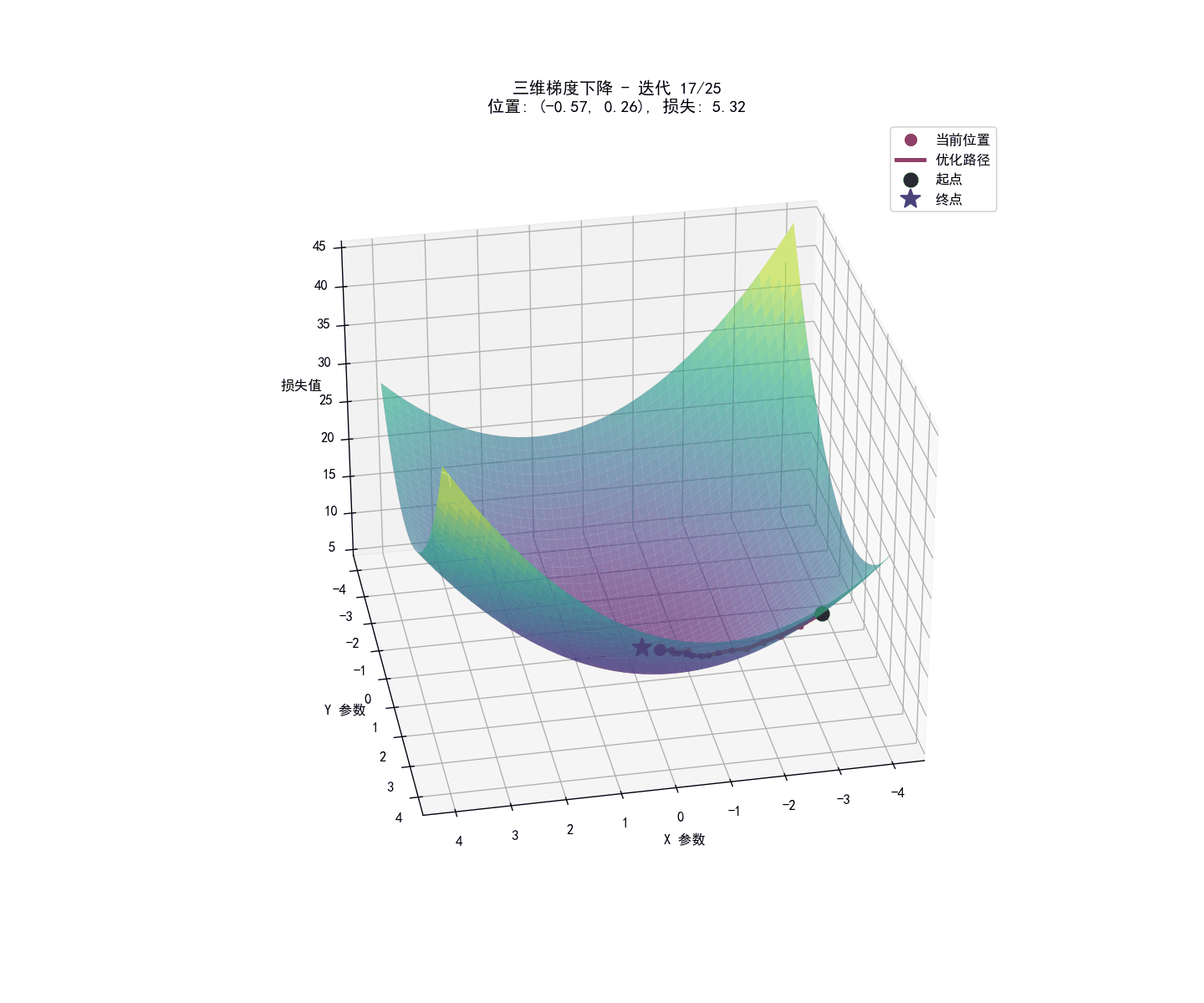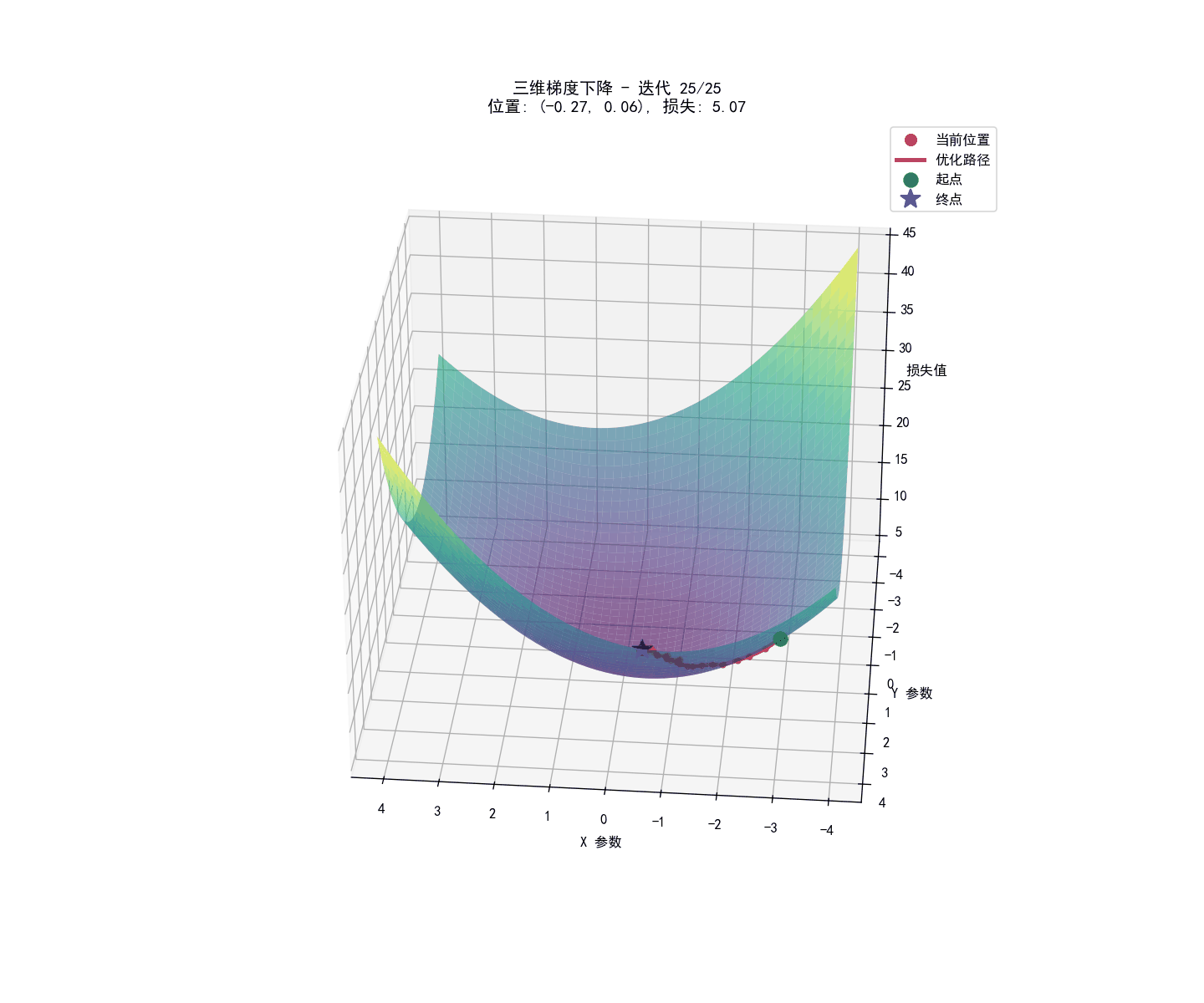
实战部分：矩阵运算与python代码

矩阵运算一般情形

假设有 m 个样本，每个样本有 n 个特征变量 x_1, x_2, \dots, x_n，加上偏置项 x_0 = 1。

矩阵定义

特征矩阵 X：维度 m \times (n+1)

参数向量 \theta：维度 (n+1) \times 1

标签向量 y：维度 m \times 1

假设函数

对每个样本的预测：

向量化（对整个数据集）：

这里 h 是 m \times 1 向量，表示每个样本的预测概率 P(y=1|x;\theta)。

代价函数

其中 \log(\cdot) 逐元素取自然对数，\theta_{1:n} 表示去掉 \theta_0 的 n \times 1 向量，\lambda 是正则化参数。

梯度下降迭代

梯度：

迭代更新：

其中 \alpha 是学习率。

展开写：

迭代过程算法步骤

1. 初始化 \theta = \mathbf{0}_{(n+1)\times 1}
2. 重复直到收敛：

   • 计算 z = X \theta （m \times 1）

   • 计算 h = \sigma(z) = 1 ./ (1 + \exp(-z)) （逐元素，m \times 1）

   • 计算误差 \text{error} = h - y （m \times 1）

   • 计算梯度：

     \text{grad} = \frac{1}{m} X^T \cdot \text{error}

     如果正则化：

     \text{grad} = \text{grad} + \frac{\lambda}{m} \begin{bmatrix} 0 \\ \theta_1 \\ \vdots \\ \theta_n \end{bmatrix}

   • 更新参数：

     \theta := \theta - \alpha \cdot \text{grad}

   • 检查收敛条件

矩阵维度小结

• X: m \times (n+1)
• \theta: (n+1) \times 1
• y: m \times 1
• z = X\theta: m \times 1
• h = \sigma(z): m \times 1
• X^T(h-y): (n+1) \times 1

具体案例分析

假设我们需要根据学生的两项成绩，来判断他们是否通过期末考核。目前我们手上有三个学生的历史数据，将其转化为特征矩阵 ：

• 第1列：偏置项（始终为1）
• 第2列：数学成绩（满分100）
• 第3列：英语成绩（满分100）

标签向量 y（1=通过，0=未通过）:

初始参数：

且令\alpha=0.2。

以第一次迭代过程为例：

• 计算线性输出 z:

• 计算预测概率 \hat{y}（Sigmoid函数）:

• 计算预测误差:

计算梯度 \nabla_w J:

• 更新参数 w:

之后周而复始，就可以逐渐逼近最佳参数了。

python代码

例题的python代码如下：

import numpy as np

# 逻辑回归梯度下降实现
class LogisticRegression:
    def __init__(self, learning_rate=0.1, max_iters=1000, tol=1e-4):
        self.learning_rate = learning_rate
        self.max_iters = max_iters
        self.tol = tol
        self.w = None
        self.loss_history = []
    
    def sigmoid(self, z):
        return 1 / (1 + np.exp(-z))
    
    def compute_loss(self, y_true, y_pred):
        # 交叉熵损失
        return -np.mean(y_true * np.log(y_pred + 1e-8) + (1 - y_true) * np.log(1 - y_pred + 1e-8))
    
    def fit(self, X, y):
        # 添加偏置项
        X = np.column_stack([np.ones(X.shape[0]), X])
        
        # 初始化参数
        self.w = np.zeros(X.shape[1])
        m = len(y)
        
        print("开始训练...")
        print(f"初始参数: w = {self.w}")
        print(f"学习率: {self.learning_rate}")
        print("-" * 50)
        
        for i in range(self.max_iters):
            # 前向传播
            z = X @ self.w
            y_pred = self.sigmoid(z)
            
            # 计算损失
            loss = self.compute_loss(y, y_pred)
            self.loss_history.append(loss)
            
            # 计算梯度
            gradient = (1/m) * X.T @ (y_pred - y)
            
            # 更新参数
            w_prev = self.w.copy()
            self.w -= self.learning_rate * gradient
            
            # 打印迭代信息
            if i < 3 or i % 100 == 0:
                print(f"迭代 {i+1}:")
                print(f"  预测值: {y_pred.round(4)}")
                print(f"  损失: {loss:.6f}")
                print(f"  梯度: {gradient.round(6)}")
                print(f"  参数: w = {self.w.round(6)}")
                print("-" * 30)
            
            # 检查收敛
            if np.linalg.norm(self.w - w_prev) < self.tol:
                print(f"在第 {i+1} 次迭代收敛")
                break
        
        return self
    
    def predict_proba(self, X):
        X = np.column_stack([np.ones(X.shape[0]), X])
        return self.sigmoid(X @ self.w)
    
    def predict(self, X, threshold=0.5):
        return (self.predict_proba(X) >= threshold).astype(int)

# 示例数据
X = np.array([
    [85, 78],  # 学生1: 数学85, 英语78 → 通过
    [62, 65],  # 学生2: 数学62, 英语65 → 未通过
    [92, 88]   # 学生3: 数学92, 英语88 → 通过
])

y = np.array([1, 0, 1])

# 创建并训练模型
model = LogisticRegression(learning_rate=0.1, max_iters=1000)
model.fit(X, y)

# 预测
print("\n=== 预测结果 ===")
y_pred_proba = model.predict_proba(X)
y_pred = model.predict(X)

for i in range(len(X)):
    print(f"学生{i+1}: 数学{X[i,0]}, 英语{X[i,1]} → "
          f"预测概率: {y_pred_proba[i]:.4f} → "
          f"预测类别: {y_pred[i]} (真实: {y[i]})")

print(f"\n最终参数: w0 = {model.w[0]:.6f}, w1 = {model.w[1]:.6f}, w2 = {model.w[2]:.6f}")