简介

概念

支持向量机，英文缩写SVM，是一种分类算法。其目的是找出一条线，或者一个超平面，将样本空间分为两部分。

与逻辑回归不同，SVM是一个几何模型，目的是为两类样本找到一个“最安全”的分离边界，使得划分尽量准确；与之相对的，逻辑回归是一个统计模型，它从概率的角度出发，致力于为所有样本找到一个“最可能”的分离方式，并且可求概率。

例子

想象一条街上放着两种物体：猫和狗。你的目标是画一条笔直的分界线，把这两种动物分开。

一个差劲的分界线画得离某些动物太近，猫或狗稍微一动就可能跑到错误的一边。
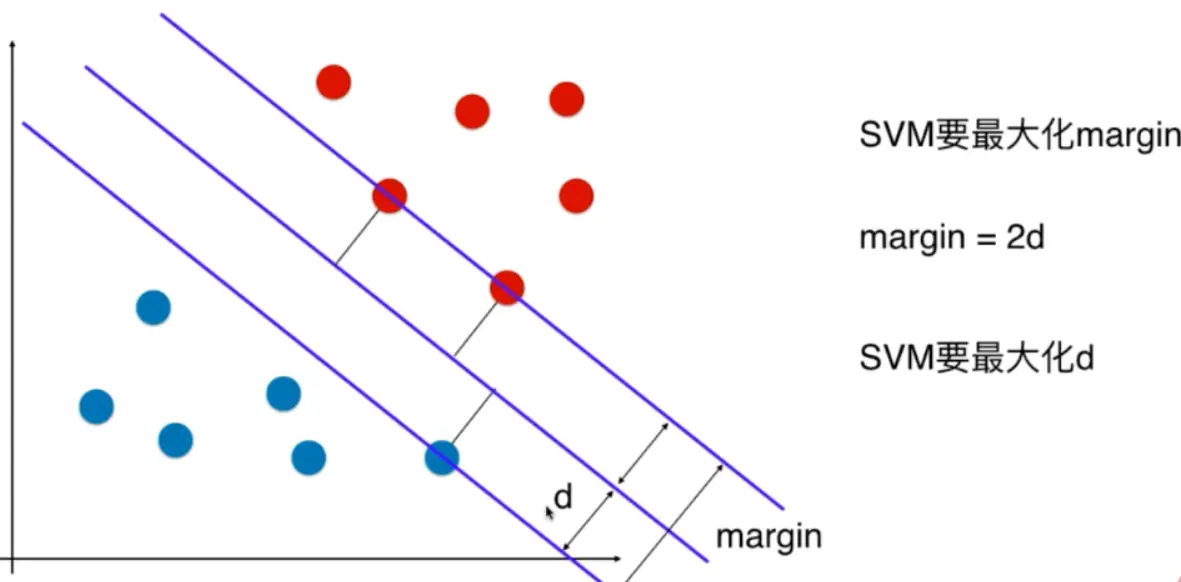
一个好的分界线应该是一条宽阔的“街道”，让两边的动物都尽可能离它远一些。这条街道的宽度，就代表了分类器的安全边际。

支持向量机就是来寻找这条“最宽街道”的算法。

• 支持向量：就是那些位于“街道”边缘的、最关键的数个数据点（比如一只特别胖的猫和一只特别靠前的狗）。它们像柱子一样“支撑”起了这条街道。如果移动这些点，街道的宽度和位置就会改变。移动其他无关的点，则不会有影响。
• 目标：SVM的核心目标就是最大化这个边际（街道的宽度），从而得到一个最稳健、泛化能力最强的分类器。

数学部分

线性可分与硬间隔

决策超平面

我们从一个简单的二分类问题开始，假设两类数据是线性可分的。目标是找到一个超平面将两类数据完美分开。

在d维空间中，一个超平面可以由以下方程定义：

对于一个样本点(\mathbf{x}_i,y_i)，其中y_{i}\in\{-1,+1\}是类别标签，正确的分类意味着：

函数间隔与几何间隔

• 函数间隔：定义为\hat{\gamma}_i=y_i(\mathbf{w}\cdot\mathbf{x}_i+b)，它代表了分类的正确性和确信度。通过放缩，值可以改变。
• 几何间隔：样本点到超平面的实际欧几里得距离。点\mathbf{x}_{i}到超平面\mathbf{w}\cdot\mathbf{x}+b=0的距离是：

值是固定的-->几何间隔是稳定且具有实际几何意义的度量。

优化目标

SVM的核心思想是最大化最靠近超平面的那个点的几何间隔（即最小几何间隔）。我们定义整个数据集的几何间隔为所有样本点几何间隔中的最小值：

我们的目标是找到\mathbf{w}和b，使得\gamma最大。

由于缩放 \mathbf{w} 和 b 不会改变超平面本身，我们可以通过缩放，使得离超平面最近的那些点（即未来的支持向量）满足：

在这个约束下，所有样本点都满足：

并且，此时的几何间隔\gamma=\frac1{||\mathbf{w}||} 。

最大化几何间隔\gamma等价于 最小化\|\mathbf{w}\|。为了方便后续求导，我们通常最小化\frac12\|\mathbf{w}\|^2。这里的\frac12是为了数学推导的便利，不影响最优解。

于是，我们得到了硬间隔SVM的原始优化问题：

这是一个经典的凸二次规划问题，保证存在全局最优解。

软间隔：处理现实世界的不完美

现实数据中常存在噪声和重叠，硬间隔的约束过于严格，容易导致过拟合，甚至在完全线性不可分时无解。为此，我们引入软间隔。

松弛变量

对每个样本点(\mathbf{x}_i,y_i)，我们引入一个松弛变量\xi_{i}\geq0，它度量了该样本违反间隔条件的程度。

• \xi_{i}=0：样本点被完美分类，且位于间隔边界之外或之上。
• 0<\xi_{i}<1：样本点被正确分类，但落在了间隔内部。
• \xi_{i}\geq1：样本点被错误分类

原来的约束条件被放松为：

新的优化问题

我们希望在最大化间隔和最小化分类错误之间找到一个平衡。因此，目标函数变为：

其中：

• \frac{1}{2}\|\mathbf{w}\|^2仍然代表最大化间隔。
• \sum_{i=1}^n\xi_i代表总的违反程度。
• C>0是一个关键的惩罚参数，控制着对错误的容忍度：
  • 值越大，对分类错误的惩罚越重，模型倾向于更小的间隔，力求分对所有点，可能导致过拟合。
  • 值越小，对错误越宽容，模型允许更宽的间隔和更多的错误，可能导致欠拟合。

完整的软间隔SVM原始优化问题为：

拉格朗日对偶与求解

上述原始问题是一个带约束的优化问题，我们使用拉格朗日乘子法将其转化为无约束问题，并推导其对偶问题，这对SVM至关重要。

拉格朗日函数

我们为两个约束条件引入拉格朗日乘子\alpha_{i}\geq0和\mu_{i}\geq0，拉格朗日函数为：

转化为对偶问题

根据拉格朗日对偶性，原始问题的解等价于先求L关于\mathbf{w},b,\boldsymbol{\xi}的极小值，再求关于\mathbf{\alpha},\mathbf{\mu}的极大值。

首先，令L对\mathbf{w},b,\boldsymbol{\xi}的偏导数为零：

1. \nabla_\mathbf{w}L=\mathbf{w}-\sum_{i=1}^n\alpha_iy_i\mathbf{x}_i=0\quad\Rightarrow\quad\mathbf{w}=\sum_{i=1}^n\alpha_iy_i\mathbf{x}_i
2. \frac{\partial L}{\partial b}=-\sum_{i=1}^n\alpha_iy_i=0\quad\Rightarrow\quad\sum_{i=1}^n\alpha_iy_i=0
3. \frac{\partial L}{\partial\xi_i}=C-\alpha_i-\mu_i=0\quad\Rightarrow\quad\mu_i=C-\alpha_i

将这三个关系式代回，得到原问题的对偶问题：

支持向量与KKT条件

解\alpha需要用到KKT（Karush-Kuhn-Tucker）最优性条件。对于软间隔SVM，KKT条件包括：

• 平稳性：\mathbf{w}=\sum_{i=1}^n\alpha_iy_i\mathbf{x}_i
• 原始可行性与对偶可行性：y_i(\mathbf{w}\cdot\mathbf{x}_i+b)\geq1-\xi_i,\quad\xi_i\geq0,\quad\alpha_i\geq0,\quad\mu_i\geq0
• 互补松弛性：
  \begin{aligned} \alpha_i[y_i(\mathbf{w}\cdot\mathbf{x}_i+b)-1+\xi_i] & =0 \\ \mu_i\xi_i & =(C-\alpha_i)\xi_i=0 \end{aligned}

根据这些条件，特别是互补松弛性，我们可以将样本点分为三类：

1. \alpha_i=0
   • 此时\mu_i=C>0，根据\mu_i\xi_i=0，有\xi_{i}=0。
   • 并且y_i(\mathbf{w}\cdot\mathbf{x}_i+b)\geq1。
   • 这些点是被正确分类且远离间隔边界的点，它们对模型\mathbf{w} 没有贡献。
2. 0<\alpha_i<C：
   • 首先，由\alpha_i[y_i(\mathbf{w}\cdot\mathbf{x}_i+b)-1+\xi_i]=0和\alpha_{i}\neq0，得y_i(\mathbf{w}\cdot\mathbf{x}_i+b)=1-\xi_i
   • 其次，由\mu_i=C-\alpha_i>0和\mu_i\xi_i=0，得\xi_{i}=0
   • 所以y_i(\mathbf{w}\cdot\mathbf{x}_i+b)=1
   • 这些点恰好落在间隔边界上，是标准的支持向量。
3. \alpha_{i}=C
   • 由\alpha_i[y_i(\mathbf{w}\cdot\mathbf{x}_i+b)-1+\xi_i]=0，得y_i(\mathbf{w}\cdot\mathbf{x}_i+b)=1-\xi_i
   • 由于\alpha_i=C，\mu_i=0，对\xi_i无约束
   • 如果0<\xi_{i}<1，点被正确分类但落在间隔内部
   • 如果\xi_{i}\geq1，点被错误分类
   • 这些点也是支持向量，它们是违反硬间隔条件的点

决策函数：在求解出\alpha后，根据\mathbf{w}=\sum_{i=1}^n\alpha_iy_i\mathbf{x}_i，新的样本\mathbf{z}的预测决策函数为：

其中偏置b可以通过任意一个满足0<\alpha_{j}<C的支持向量计算得到：b=y_j-\mathbf{w}\cdot\mathbf{x}_j

关键洞察：最终的模型和决策函数只依赖于支持向量(\alpha_i>0\text{ 的点})，与其他样本无关。这赋予了SVM天然的抗干扰能力和内存效率。

核函数

为什么需要核函数？

问题：在原始的低维输入空间中，数据可能是线性不可分的（例如，无法用一条直线分开）。

直觉解决方案：将数据映射到一个更高维、甚至无限维的特征空间。在这个新的空间中，数据可能会变得线性可分。

面临的挑战：

1. 计算成本：直接计算高维映射\phi本身可能计算量极大。如果特征空间维度非常高，甚至无限维，这在计算上是不可行的。
2. 存储成本：存储高维的\phi 需要大量内存。

核函数的精妙之处：它允许我们在不真正计算高维映射\phi的情况下，直接计算出高维空间中的内积结果。

核函数的定义与原理

给定一个映射\phi:\mathcal{X}\to\mathcal{H}，将数据从输入空间\mathcal{X}映射到特征空间\mathcal{H}。一个函数K被称为核函数，如果对于所有\mathbf{x}_{i},\mathbf{x}_{j}\in\mathcal{X}，它满足：

其中\langle\cdot,\cdot\rangle_\mathcal{H}表示在特征空间\mathcal{H}的内积

关键点：我们只关心K(\mathbf{x}_i,\mathbf{x}_j)的计算结果，而完全不需要知道\phi具体是什么

一个例子

假设我们在二维空间\mathbf{x}=(x_1,x_2)，考虑一个映射到三维空间的函数：

现在，我们计算两个向量\mathbf{x}=(x_1,x_2)和\mathbf{z}=(z_1,z_2) 在这个三维特征空间中的内积：

发现：

• 左边：我们进行了复杂的映射，然后在三维空间计算了内积。
• 右边：我们直接在原始二维空间计算了内积(\mathbf{x}\cdot\mathbf{z})，然后平方。
• 结果完全相等：\langle\phi(\mathbf{x}),\phi(\mathbf{z})\rangle=(\mathbf{x}\cdot\mathbf{z})^2

这意味着，核函数K(\mathbf{x},\mathbf{z})=(\mathbf{x}\cdot\mathbf{z})^2隐式地对应了上述从二维到三维的映射\phi。我们通过一个在原始空间O(d^2)的计算，等价地获得了在特征空间O(d^2)中进行映射和内积计算的结果，节省了计算和存储映射后向量的开销。

常见的核函数

1. 线性核：K(\mathbf{x}_i,\mathbf{x}_j)=\mathbf{x}_i\cdot\mathbf{x}_j，恒等映射，特征空间就是原始输入空间。
2. 多项式核：K(\mathbf{x}_i,\mathbf{x}_j)=(\gamma\mathbf{x}_i\cdot\mathbf{x}_j+r)^d

• 参数：
  • d：多项式的次数，控制着映射后空间的复杂度。d越大，模型越复杂，越容易过拟合。
  • \gamma（缩放因子）、r（常数项）：通常作为超参数进行调优。
• 特点：多项式核能够学习全局的、多项式形式的非线性模型。当d=1且r=0时，它退化为线性核。
• 适用场景：适用于所有特征大体上是同等重要的场景。但由于其数值稳定性较差（当d很大时，内积可能趋于无穷大或无穷小），在实践中不如RBF核常用。

3. 高斯镜像基函数核：K(\mathbf{x}_i,\mathbf{x}_j)=\exp(-\gamma\|\mathbf{x}_i-\mathbf{x}_j\|^2)

• 参数：
  • \gamma >0：一个至关重要的参数。它控制了单个训练样本的影响范围。
    • \gamma 越大，高斯函数越“瘦”，只有非常近的样本点才会被强烈影响，决策边界变得非常复杂、曲折，可能导致过拟合。
    • \gamma 越小，高斯函数越“胖”，远处样本的影响也越大，决策边界越平滑，可能导致欠拟合。
• 对应的映射：它隐式地映射到了一个无限维的特征空间。这是它强大表达能力的来源。
• 特点：这是最常用、最强大的非线性核。它具有局部性，每个支持向量只影响其邻近区域的决策边界。数值稳定性好。

3. Sigmoid核：K(\mathbf{x}_i,\mathbf{x}_j)=\tanh(\gamma\mathbf{x}_i\cdot\mathbf{x}_j+r)

• 特点：从形式上看，它类似于神经网络中的激活函数。在某些参数下，SVM模型等价于一个没有隐层的神经网络。
• 注意：Sigmoid核并不总是满足Mercer条件（即核矩阵不一定半正定），这可能导致训练过程不收敛。因此，它的使用不如多项式核和RBF核普遍。

python实战部分

基础示例

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import classification_report, confusion_matrix

# 加载鸢尾花数据集，只取前两类实现二分类
iris = datasets.load_iris()
X = iris.data[:100, :2]  # 只取前两个特征方便可视化
y = iris.target[:100]

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建线性SVM分类器
svm_linear = SVC(kernel='linear', C=1.0)
svm_linear.fit(X_train, y_train)

# 预测和评估
y_pred = svm_linear.predict(X_test)
print("分类报告:")
print(classification_report(y_test, y_pred))

# 可视化决策边界
def plot_decision_boundary(clf, X, y):
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                         np.arange(y_min, y_max, 0.02))
    
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    
    plt.contourf(xx, yy, Z, alpha=0.4)
    plt.scatter(X[:, 0], X[:, 1], c=y, alpha=0.8)
    plt.xlabel('Feature 1')
    plt.ylabel('Feature 2')
    plt.title('SVM Decision Boundary')
    plt.show()

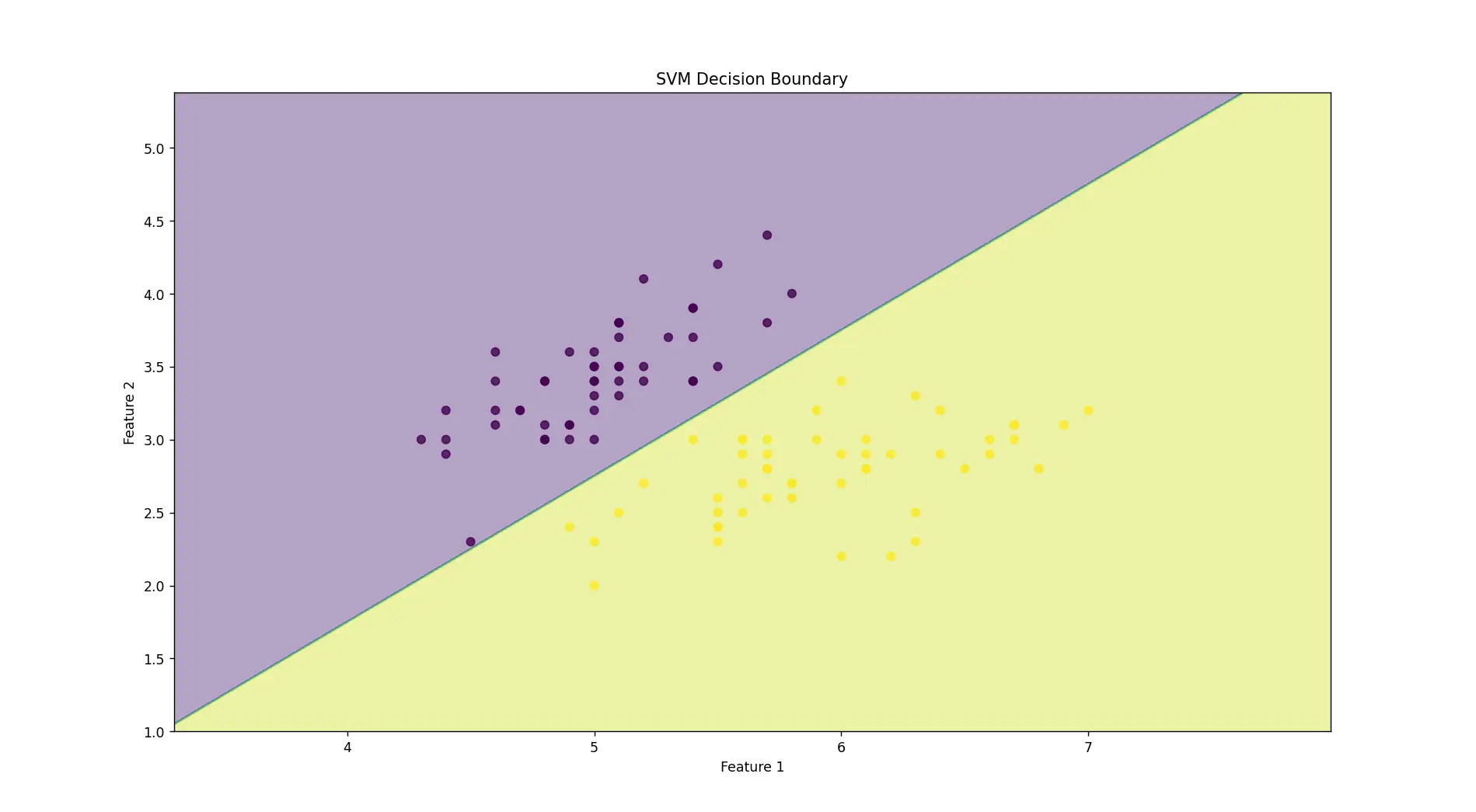
plot_decision_boundary(svm_linear, X, y)

运行结果如下：

非线性SVM与不同核函数比较

# kernel_comparison.py
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.svm import SVC

# 创建非线性数据集
X_moons, y_moons = make_moons(n_samples=200, noise=0.1, random_state=42)

# 定义不同核函数的SVM
kernels = ['linear', 'poly', 'rbf', 'sigmoid']
classifiers = {}

for kernel in kernels:
    if kernel == 'poly':
        classifiers[kernel] = SVC(kernel=kernel, degree=3, C=1.0)
    elif kernel == 'rbf':
        classifiers[kernel] = SVC(kernel=kernel, gamma='scale', C=1.0)
    else:
        classifiers[kernel] = SVC(kernel=kernel, C=1.0)

# 在月亮形数据上比较不同核函数
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
axes = axes.ravel()

for idx, (name, clf) in enumerate(classifiers.items()):
    clf.fit(X_moons, y_moons)
    
    # 创建网格点
    x_min, x_max = X_moons[:, 0].min() - 0.5, X_moons[:, 0].max() + 0.5
    y_min, y_max = X_moons[:, 1].min() - 0.5, X_moons[:, 1].max() + 0.5
    xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
                         np.linspace(y_min, y_max, 100))
    
    # 预测每个网格点
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    
    # 绘制决策边界
    axes[idx].contourf(xx, yy, Z, alpha=0.4)
    axes[idx].scatter(X_moons[:, 0], X_moons[:, 1], c=y_moons, alpha=0.8)
    axes[idx].set_title(f'SVM with {name.upper()} kernel')
    axes[idx].set_xlabel('Feature 1')
    axes[idx].set_ylabel('Feature 2')

plt.tight_layout()
plt.show()

运行结果如下：

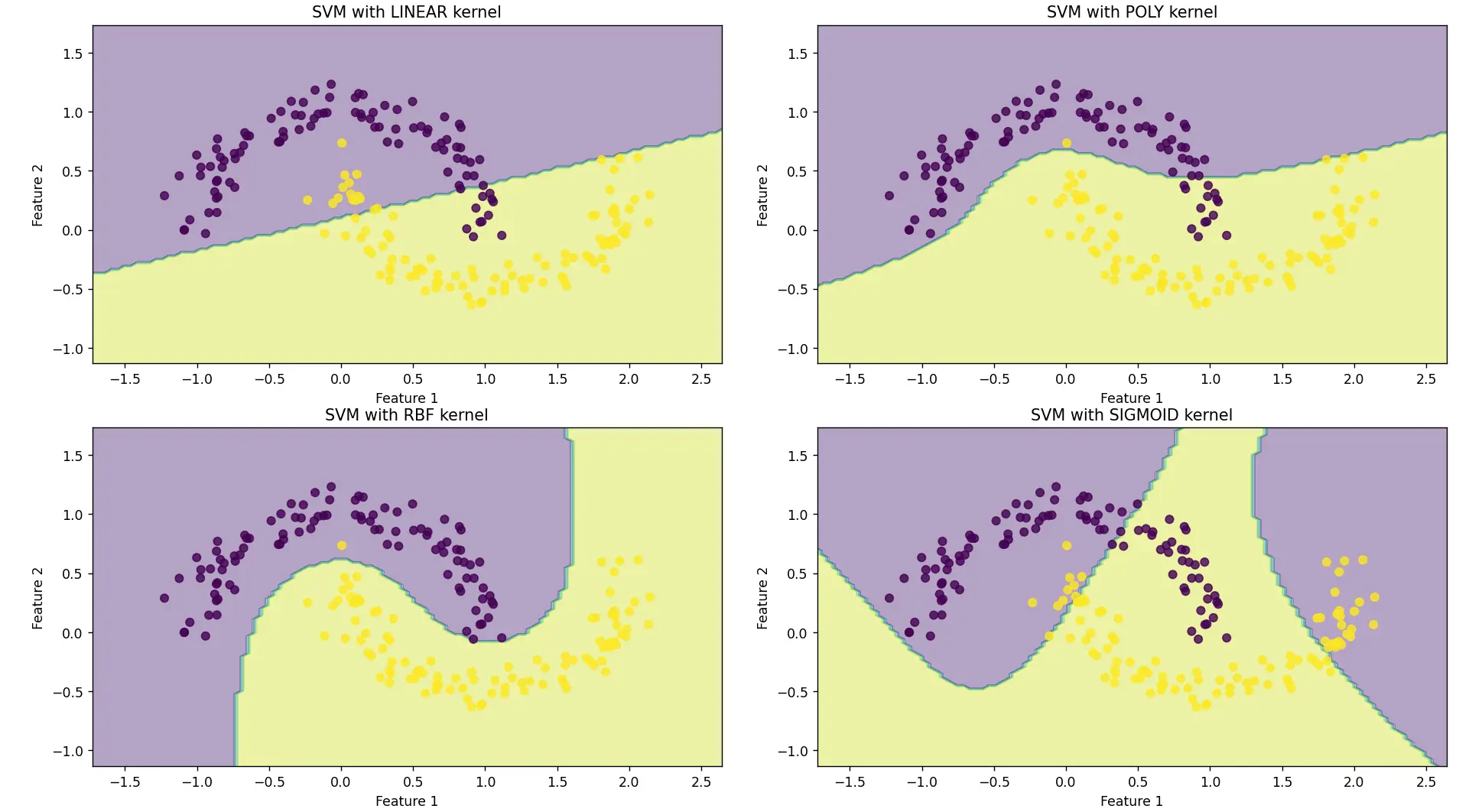
超参数调优实战

# hyperparameter_tuning.py
import numpy as np
from sklearn.datasets import make_moons
from sklearn.model_selection import GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC

# 使用更复杂的数据集
X, y = make_moons(n_samples=300, noise=0.2, random_state=42)

# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 定义参数网格
param_grid = {
    'C': [0.1, 1, 10, 100],
    'gamma': ['scale', 'auto', 0.1, 1, 10],
    'kernel': ['rbf', 'poly', 'sigmoid']
}

# 网格搜索
grid_search = GridSearchCV(
    SVC(), 
    param_grid, 
    cv=5, 
    scoring='accuracy',
    n_jobs=-1
)

grid_search.fit(X_scaled, y)

print("最佳参数:", grid_search.best_params_)
print("最佳交叉验证分数:", grid_search.best_score_)

# 使用最佳参数训练最终模型
best_svm = grid_search.best_estimator_
print("最佳模型:", best_svm)

得到结果：

最佳参数: {'C': 1, 'gamma': 1, 'kernel': 'rbf'}
最佳交叉验证分数: 0.9633333333333333
最佳模型: SVC(C=1, gamma=1)

支持向量分析

# support_vectors_analysis.py
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC

# 使用月亮形数据集
X, y = make_moons(n_samples=300, noise=0.2, random_state=42)

# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 使用RBF SVM
svm_rbf = SVC(kernel='rbf', C=10, gamma=0.1)
svm_rbf.fit(X_scaled, y)

# 获取支持向量
support_vectors = svm_rbf.support_vectors_
support_vector_indices = svm_rbf.support_

print(f"支持向量数量: {len(support_vectors)}")
print(f"支持向量索引: {support_vector_indices[:10]}")  # 只显示前10个

# 可视化支持向量
plt.figure(figsize=(10, 8))

# 创建网格点
x_min, x_max = X_scaled[:, 0].min() - 0.5, X_scaled[:, 0].max() + 0.5
y_min, y_max = X_scaled[:, 1].min() - 0.5, X_scaled[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
                     np.linspace(y_min, y_max, 100))

# 预测每个网格点
Z = svm_rbf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# 绘制决策边界和支持向量
plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=y, alpha=0.6, label='Data points')
plt.scatter(support_vectors[:, 0], support_vectors[:, 1], 
            s=100, facecolors='none', edgecolors='red', 
            linewidths=2, label='Support Vectors')
plt.xlabel('Feature 1 (scaled)')
plt.ylabel('Feature 2 (scaled)')
plt.title('SVM with RBF Kernel - Support Vectors Highlighted')
plt.legend()
plt.show()

结果如下：

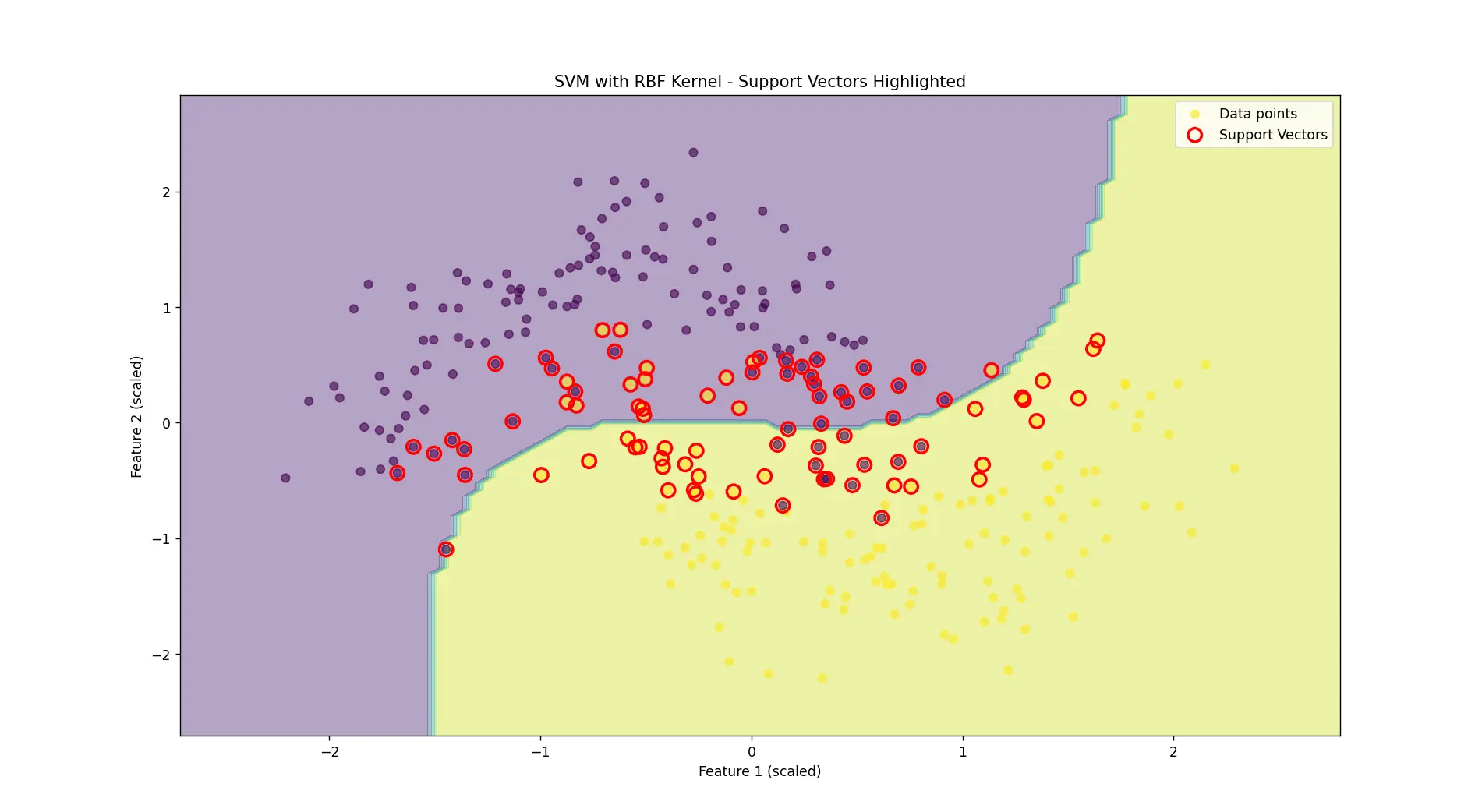
多分类SVM

# multiclass_svm.py
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import classification_report, confusion_matrix

# 加载完整的鸢尾花数据集（3类）
iris = load_iris()
X, y = iris.data, iris.target

# 划分训练测试集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42, stratify=y
)

# 多分类SVM - scikit-learn自动使用一对一策略
svm_multi = SVC(kernel='rbf', C=1.0, gamma='scale', decision_function_shape='ovr')
svm_multi.fit(X_train, y_train)

# 预测和评估
y_pred = svm_multi.predict(X_test)

print("多分类SVM性能:")
print(classification_report(y_test, y_pred, target_names=iris.target_names))

# 混淆矩阵
cm = confusion_matrix(y_test, y_pred)
print("混淆矩阵:")
print(cm)

# 准确率
accuracy = svm_multi.score(X_test, y_test)
print(f"测试集准确率: {accuracy:.4f}")

运行结果如下：

多分类SVM性能:
              precision    recall  f1-score   support

      setosa       1.00      1.00      1.00        15
  versicolor       0.93      0.93      0.93        15
   virginica       0.93      0.93      0.93        15

    accuracy                           0.96        45
   macro avg       0.96      0.96      0.96        45
weighted avg       0.96      0.96      0.96        45

混淆矩阵:
[[15  0  0]
 [ 0 14  1]
 [ 0  1 14]]
测试集准确率: 0.9556

自定义核函数

# custom_kernel.py
import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score

# 创建分类数据集
X, y = make_classification(n_samples=100, n_features=2, n_redundant=0, 
                          n_informative=2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 自定义RBF核函数
def my_rbf_kernel(X, Y=None, gamma=0.1):
    """
    自定义RBF核函数实现
    """
    if Y is None:
        Y = X
    K = np.zeros((X.shape[0], Y.shape[0]))
    for i, x_i in enumerate(X):
        for j, x_j in enumerate(Y):
            K[i, j] = np.exp(-gamma * np.linalg.norm(x_i - x_j)**2)
    return K

# 使用自定义核函数
svm_custom = SVC(kernel=my_rbf_kernel)
svm_custom.fit(X_train, y_train)

# 比较自定义核与内置核的性能
custom_score = svm_custom.score(X_test, y_test)
builtin_score = SVC(kernel='rbf', gamma=0.1).fit(X_train, y_train).score(X_test, y_test)

print(f"自定义RBF核准确率: {custom_score:.4f}")
print(f"内置RBF核准确率: {builtin_score:.4f}")

# 预测示例
y_pred_custom = svm_custom.predict(X_test)
y_pred_builtin = SVC(kernel='rbf', gamma=0.1).fit(X_train, y_train).predict(X_test)

print("\n前10个预测结果比较:")
print("自定义核:", y_pred_custom[:10])
print("内置核:  ", y_pred_builtin[:10])

运行结果如下：

自定义RBF核准确率: 0.9667
内置RBF核准确率: 0.9667

前10个预测结果比较:
自定义核: [0 1 1 0 1 0 0 0 1 1]
内置核:   [0 1 1 0 1 0 0 0 1 1]

关键参数说明

• C: 惩罚参数，控制对错误分类的容忍度
• kernel: 核函数类型（linear, poly, rbf, sigmoid等）
• gamma: RBF、多项式、sigmoid核的参数
• degree: 多项式核的次数
• probability: 是否启用概率估计